サンプリング法

標本調査は調査対象の一部を調べて全体を知ろうとするものですから、 デタラメに標本を抽出していては調査結果自体もデタラメな ものになっ てしまうため標本の抽出にはいくつかのルールがあります。 それが サンプリング法と呼ばれるものです。

調査は大きく分けて国勢調査に代表される「全数調査（悉皆調査）」と「標本調査」があります。一般に実施されている調査の殆どは「標本調査」で行われています。正しいデータを得ようとすると、全数調査が一番いいのですがこれを実施するには膨大な費用と時間が必要です。これらの効率を考えた場合、全数調査が最上の調査方法であるとはいえません。

しかし、標本調査は調査対象の一部を調べて全体を知ろうとするものですから、デタラメに標本を抽出していては調査結果自体もデタラメなものになってしまうため標本の抽出にはいくつかのルールがあります。それがサンプリング法と呼ばれるものです。 サンプリング法は大きく分けて「有意抽出法」「無作為抽出法」「クォータ・サンプリング」の３つがあります。

有意抽出法

有意抽出法とは、身近な人や調査しやすい人などを対象者にするなど、調査者が適当に対象者を選ぶ方法です。この方法は一般的な結論を得るために用いられるのではなく、例えば本調査を行う前の予備調査・プリテストなど、本調査実施前に、事前に検討をするための情報を得る時などに用いられます。

これは後述の無作為抽出で得られたサンプルでの調査結果が統計学に基づき誤差が把握できるのに対し、有意抽出では精度の保証はなく、調査結果が意味あるものになるか否かはすべてデータの解釈次第ということになるからです。

無作為抽出法

標本理論の基本は、ある調査対象者の全集団（母集団）からその一部の対象者（標本）を抽出し、調査することにより、標本のみならず母集団について「一定の誤差範囲内で」推定を行うことができるというものです。 無作為抽出法はランダムダンプリングとも呼ばれます。ランダムという言葉からデタラメ」にサンプルを選ぶことと誤解されますが、統計用語のランダム・サンプリングはデタラメどころか極めて厳格に少数の標本によって母集団の正確な縮図が得られるようサンプリングを行うことを意味しています。

無作為抽出には極めて厳格な手続きが求められますが、こうして得られたサンプルでの調査結果は統計学に基づき誤差が把握でき、データの精度に保証が与えられます。 サンプリングの具体的方法には以下のようなものがあります。

「単純無作為抽出」

母集団の全構成員に番号を振り、抽出する標本の数だけ乱数表を引いて、その番号に対応した個人を標本として抽出するもの。

「系統抽出」

等間隔抽出法とも呼ばれ、何人おきといった具合にサンプルを選ぶ方法。例えば従業員２万人の工場で1000人のランダムサンプルを取る場合、２万人を１列にならべ20人おきに取っていけば、1000人の標本が得られる。 実際の調査では調査対象の母集団は何万・何千万といった数になり、上記のような方法は実施不可能です。そこで以下の「多段抽出」が使用されます。

「多段抽出」

全調査地域の中からいくつかの調査地点をまず選択し、その地点から調査対象者を選び出す二段抽出はよく使用される方法です。多段抽出で地点と個人を選び出す方法には「等確立抽出法」と「確立比例抽出法」の2つがあり、前者は選択した地点の人口比に対応させて個人を選択する方法、後者は各地点の人口を同一にし、それぞれから同数の個人を抽出する方法です。

「層化抽出」

一般消費者であれば対象者を性・年齢・居住地域などで層化しておき、それぞれの層の大きさに比例するように地点・個人を抽出する方法です。どんな抽出法をとるにせよ層化をする方がしないより常に調査の精度は良いことが統計的に証明されています。

クォータサンプリング

クォータ・サンプリングは有意抽出法の変形で、性別や年令層を母集団の比率に合わせるなど（男女を半々にする、20代・30代・40代などの構成を母集団の構成比にあわせる）の配慮はするが、その他は有意抽出するというものです。米国では主流のサンプリング方法ですが、基本的には有意抽出と同様の難点をもつため、比較的小サンプル（Ｎ＝100～200）の質的調査に用いられます。

必要なサンプル数

前述のサンプリングの項で標本理論の基本は、母集団について「一定の誤差範囲内で」推定を行うことができることと述べましたが、実際に調査を実施するためサンプル数をいくつにするか検討するとき、基準になるのは「どの程度の誤差を許容するか」ということです。標本調査では以下の公式から必要なサンプル数を決定します。

必要なサンプル数＝（Ｋ／Ｅ）＾２＊Ｐ＊（１００－Ｐ）

（※母集団の規模が大きい場合）
有意水準(K)（95%のとき1.96、99%のとき2.58）
目標誤差(E)
母比率の推定値(P)

ex.母比率50％　目標誤差５％　有意水準95％の場合　サンプル数＝384

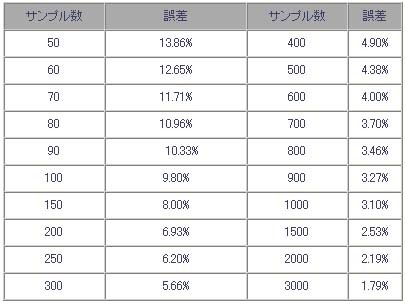
この数式はサンプル数の決定だけでなく、調査の結果得られた値が どの程度信頼できるかを推定する場合にも用いられます。

比率の標準誤差早見表 （信頼係数95％、母比率の推定値50%）

[PREV]　｜　[NEXT]